
이 글은 Deep RL Course를 학습하고 정리한 글입니다.
정책 그래디언트 더 깊이 파헤치기
🖼 큰 그림 그리기
정책 그래디언트(Policy-Gradient) 방법은 기대 보상을 최대화하는 파라미터 $\theta$ 를 찾는 것을 목표로 합니다. 파라미터화된 확률론적 정책을 사용합니다. 즉, 신경망이 각 행동에 대한 확률 분포를 출력합니다. 특정 행동을 선택할 확률을 행동 선호도(Action Preference)라고 합니다.
CartPole-v1 예제
- 입력: 환경의 상태
- 출력: 해당 상태에 대한 행동 확률 분포

정책 그래디언트의 목표
정책 그래디언트의 목표는 행동의 확률 분포를 제어하는 것입니다. 즉, 보상을 최대화하는 좋은 행동이 미래에 더 자주 샘플링되도록 정책을 조정하는 것입니다. 에이전트가 환경과 상호작용하면서 좋은 행동을 더 자주 선택하도록 파라미터를 미세 조정합니다.
가중치를 최적화하는 방법
핵심적인 아이디어는 에이전트가 에피소드 동안 환경과 상호작용하도록 하는 것입니다. 만약 에이전트가 에피소드에서 이겼다면 해당 에피소드에서 수행한 모든 행동이 좋은 행동이라고 간주합니다. 따라서 해당 상태-행동 쌍의 확률 $P(a|s)$를 증가시킵니다. 반대로 실패했다면 해당 행동들의 확률을 감소시킵니다.
아래는 정책 그래디언트 알고리즘을 간단히 나타낸 것입니다.
1. 정책 $\pi$를 사용하여 에피소드를 수집합니다.
2. 보상을 계산합니다.
3. 정책의 가중치를 업데이트합니다.
- 보상이 양수(Positive): 에피소드 동안 수행된 모든 상태-행동 쌍의 확률을 증가시킴
- 보상이 음수(Negative): 에피소드 동안 수행된 모든 상태-행동 쌍의 확률을 감소시킴
🏊♀️ 정책 그래디언트 더 깊이 파헤쳐보기
1. 확률론적 정책 (Stochastic Policy)
정책 $\pi$는 파라미터 $\theta$를 가지고 있으며, 주어진 상태 $s$에 대해 행동 $a$의 확률 분포를 출력합니다.

즉, 정책 $\pi$는 특정 상태에서의 행동 선택 확률 분포를 나타냅니다.
2. 목적 함수 (Objective Function)
정책이 얼마나 좋은지를 평가하기 위해 목적 함수(Objective Function)를 정의해야 합니다. 이 함수는 정책의 성능을 측정하는 역할을 하며 기대 누적 보상(Expected Cumulative Return)을 출력합니다.
목표 함수는 에이전트의 궤적(Trajectory)을 기반으로 정책의 성능을 평가합니다. 여기서 궤적이란 보상을 고려하지 않은 상태-행동 시퀀스입니다.

- $R(\tau)$: 특정 궤적 $\tau$에 대한 누적 보상
- $\mathbb{E}_{\tau \sim \pi}$: 정책 $\pi$에 따라 생성된 궤적 $\tau$에 대한 기댓값
즉, 정책이 생성할 수 있는 모든 궤적에 대한 기대 보상의 평균을 계산합니다.

- $R(\tau)$: 해당 궤적에서 얻을 수 있는 누적 보상
- $P(\tau;\theta)$: 특정 궤적 $\tau$가 발생할 확률
- $\sum\limits_{\tau}$: 가능한 모든 궤적에 대한 합
즉, 모든 가능한 궤적에 대해 그 궤적이 발생할 확률 $P(\tau;\theta)$과 보상 $R(\tau)$의 곱을 합산하여 정책 $\pi_{\theta}$의 성능을 평가합니다.

- $P(\tau; \theta)$: 특정 궤적 $\tau$가 발생할 확률
- $\pi_{\theta}(a_t|s_t)$: 상태 $s_t$에서 행동 $a_t$를 선택할 확률
- $P(s_{t+1}|s_t, a_t)$: 환경의 상태 전이 확률 (Environment dynamics)
즉, 정책이 선택하는 행동의 확률과 환경의 상태 전이 확률을 조합하여 전체 궤적의 확률을 계산합니다. 이를 통해 정책 $\pi_{\theta}$를 조정하여 궤적의 확률을 변화시킬 수 있습니다.

최적화의 목표는 정책의 파라미터 $\theta$를 조정하여 기대 누적 보상 $J(\theta)$를 최대화하는 것입니다. 즉, 좋은 행동이 더 자주 선택되도록 정책을 학습하는 것이 정책 그래디언트 방법의 핵심 목표입니다.
📝 정책 그래디언트 정리
정책 그래디언트 방법에서는 정책의 파라미터 $\theta$를 최적화하여 기대 보상 $J(\theta)$을 최대화하는 것이 목표입니다. 이를 위해 경사 상승법(Gradient Ascent)을 사용합니다.
1. 경사 상승법 (Gradient Ascent)
경사 상승법(Gradient Ascent)은 목적 함수를 최대화하는 방향으로 파라미터를 업데이트하는 기법입니다. 이는 경사 하강법(Gradient Descent)와 반대 개념으로 함수의 기울기가 가장 급격하게 증가하는 방향을 따릅니다.
$$\theta \leftarrow \theta + \alpha \Delta_\theta J(\theta)$$
- $\theta$: 정책의 파라미터
- $\alpha$: 학습률
- $\Delta_\theta J(\theta)$: $\theta$에 대한 목표 함수의 그래디언트
즉, 파라미터 $\theta$를 반복적으로 업데이트하면서 정책이 기대 보상을 최대화하도록 학습합니다.
2. 정책 그래디언트의 문제점
Gradient Ascent를 적용하려면 목적 함수 $J(\theta)$의 그래디언트 $\Delta_{\theta} J(\theta)$를 계산해야 합니다. 하지만 여기서 두 가지 문제가 발생합니다.

(1) 궤적 확률 $P(\tau; \theta)$ 계산의 어려움
$P(\tau;\theta)$는 정책이 생성할 수 있는 모든 궤적의 확률입니다. 이를 정확히 계산하려면 가능한 모든 상태와 행동 조합을 고려해야 하므로 연산 비용이 매우 큽니다.
(2) 상태 분포(State Distribution)의 미분 문제
목적 함수 $J(\theta)$를 미분하기 위해서는 마르코프 결정 과정(Markov Decision Process, MDP)라고 하는 상태 분포를 미분해야 합니다. 환경이 결정하는 확률이므로 환경의 동적 특성을 정확히 알지 못하는 경우 이를 미분하는 것이 불가능합니다.
3. 정책 그래디언트 정리 (Policy Gradient Theorem)
위 문제를 해결하기 위해 정책 그래디언트 정리(Policy Gradient Theorem)를 사용합니다.

이 식을 통해 환경의 상태 분포를 직접 미분하지 않고도 정책의 그래디언트를 구할 수 있습니다.
🔨 REINFORCE 알고리즘
REINFORCE 알고리즘(또는 Monte-Carlo Policy-Gradient)은 정책 그래디언트 방법 중 하나로, 한 에피소드 전체에서 얻은 누적 보상을 기반으로 정책 파라미터 $\theta$를 업데이트하는 방법입니다.
1. REINFORCE 알고리즘 개요
REINFORCE 알고리즘은 다음 단계를 반복하여 정책을 최적화합니다.
1. 정책 $\pi_\theta$를 사용하여 하나의 에피소드 $\tau$를 수집
2. 수집된 에피소드를 기반으로 그래디언트 $\hat{g} = \Delta_\theta J(\theta)$을 추정
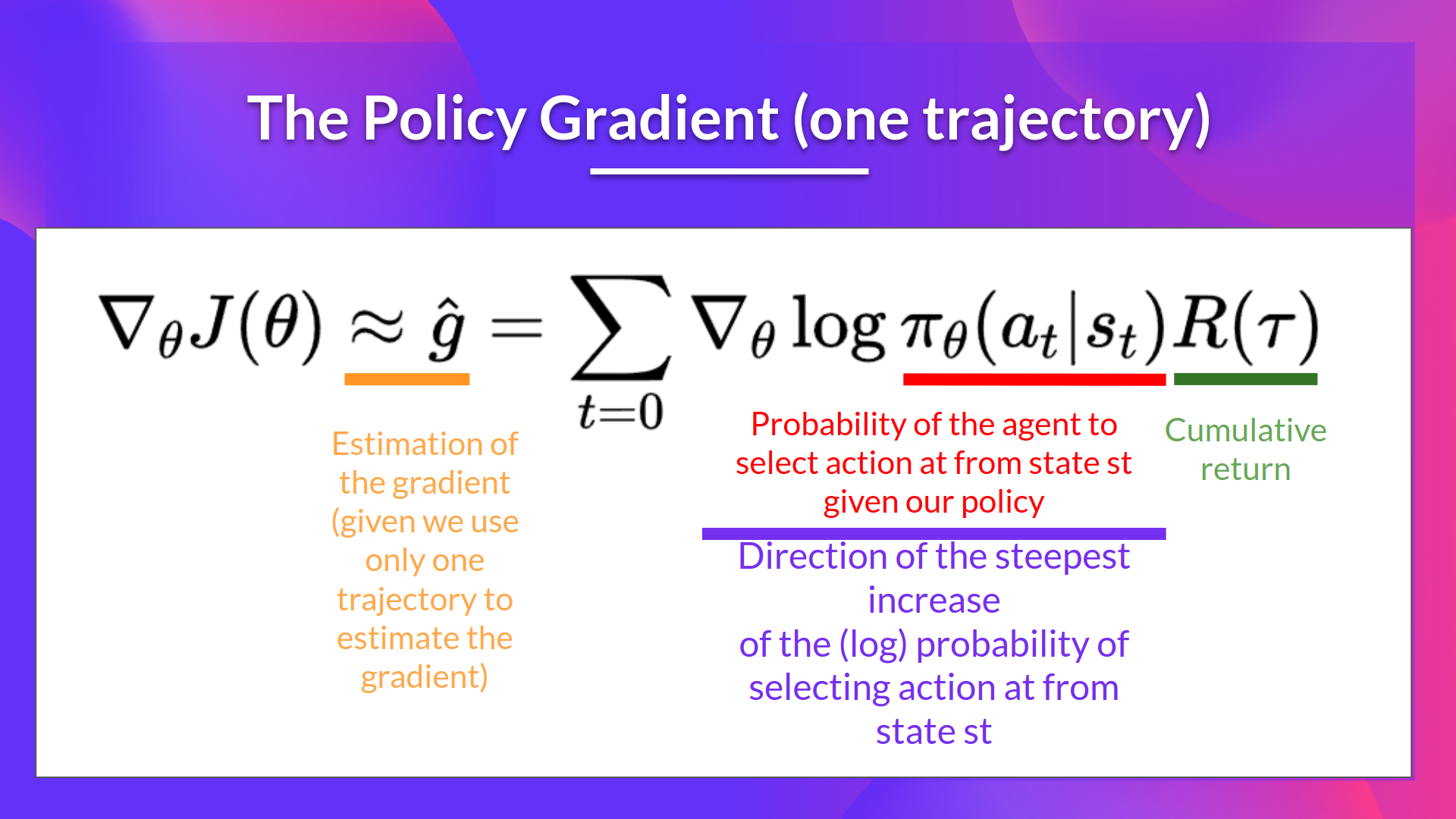
3. 정책 파라미터 $\theta$를 업데이트 $\theta \leftarrow \theta + \alpha \hat{g}$
2. 정책 업데이트의 해석
(1) 정책 확률의 기울기 $\Delta_\theta \log \pi_\theta$
특정 행동 $a_t$의 선택 확률을 변화시키는 방향을 나타냅니다. 높은 보상을 받은 행동의 확률을 증가시키고 낮은 보상을 받은 행동의 확률을 감소시키는 역할을 합니다.
(2) 누적 보상 $R_\tau$
보상의 크기가 크면 해당 행동을 더 자주 선택하도록 강화하고 보상의 크기가 작으면 해당 행동이 덜 선택되도록 조정합니다. 즉, 좋은 행동은 강화하고 나쁜 행동은 억제하는 방식으로 학습이 진행됩니다.
3. 다중 궤적을 통한 그래디언트 추정
하나의 에피소드만을 사용하여 정책을 업데이트할 경우 변동성(Variance)이 높아져 학습이 불안정할 수 있습니다. 여러 개의 에피소드를 수집하여 평균을 내어 그래디언트를 추정하면 변동성을 줄이고 학습을 더 안정적으로 수행할 수 있습니다. 이를 통해 노이즈를 감소시키고 정확한 그래디언트 방향을 추정할 수 있습니다.

'강화학습' 카테고리의 다른 글
| [강화학습/심층강화학습 특강] 다중 슬롯머신 - 톰슨 샘플링 모델 (1) (0) | 2025.02.21 |
|---|---|
| [강화학습/심층강화학습 특강] 강화학습의 5가지 원칙 (0) | 2025.02.18 |
| [Deep RL Course] 정책 기반 (Policy-based) 강화 학습 (1) | 2025.01.22 |
| [Deep RL Course] 하이퍼파라미터 최적화 - Optuna (0) | 2025.01.21 |
| [Deep RL Course] DQN 실습 - Atari 게임 (0) | 2025.01.20 |