728x90

백준 1935번: 후위 표기식2
📌 문제
후위 표기식과 각 피연산자에 대응하는 값들이 주어져 있을 때, 그 식을 계산하는 프로그램을 작성하시오.
입력
첫째 줄에 피연산자의 개수(1 ≤ N ≤ 26) 가 주어진다.
둘째 줄에는 후위 표기식이 주어진다. (여기서 피연산자는 A~Z의 영대문자이며, A부터 순서대로 N개의 영대문자만이 사용되며, 길이는 100을 넘지 않는다)
셋째 줄부터 N+2번째 줄까지는 각 피연산자에 대응하는 값이 주어진다.
3번째 줄에는 A에 해당하는 값, 4번째 줄에는 B에 해당하는값 , 5번째 줄에는 C ...이 주어진다,
피연산자에 대응 하는 값은 100보다 작거나 같은 자연수이다.
후위 표기식을 앞에서부터 계산했을 때, 식의 결과와 중간 결과가 -20억보다 크거나 같고, 20억보다 작거나 같은 입력만 주어진다.
출력
계산 결과를 소숫점 둘째 자리까지 출력한다.
📝 문제 접근 방법
후위 표기식(Postfix Notation)
연산자(+, -, *, / 등)가 피연산자(숫자나 변수( 뒤에 위치하는 수식 표기 방식
- 예: 중위 표기식(Infix Notation) A + B → 후위 표기식 A B +
- 수식의 연산 우선순위를 명시하지 않아도 되기 때문에 중위 표기식과 달리 괄호가 필요 없습니다.
아이디어
후위 표기식의 연산을 스택을 이용해 계산
- 피연산자의 값을 저장하기
- 문제에서 각 피연산자(A, B, C 등)에 대응하는 값이 주어지는데 이를 배열이나 딕셔너리에 저장해 후위 표기식을 처리할 때 빠르게 참조할 수 있도록 합니다.
- 예를 들어 A의 값이 1이라면 {A: 1}로 저장해둡니다.
- 후위 표기식 순회하면서 스택에 값 쌓기
- 후위 표기식의 각 문자를 하나씩 순회하면서 피연산자와 연산자를 처리합니다.
- 피연산자(A ~ Z): 피연산자를 만나면 해당 값을 스택에 푸시합니다.
- 연산자(+, -, *, /): 연산자를 만나면 스택에서 2개의 피연산자를 꺼내 해당 연산을 수행하고 결과를 다시 스택에 넣습니다.
- 이 과정을 후위 표기식의 끝까지 반복하며 최종적으로 스택에 남은 값이 전체 수식의 계산 결과가 됩니다.
예제
- 피연산자의 개수: 5
- 후위 표기식: ABC*+DE/-
- 피연산자 값: A = 1, B = 2, C = 3, D = 4, E = 5
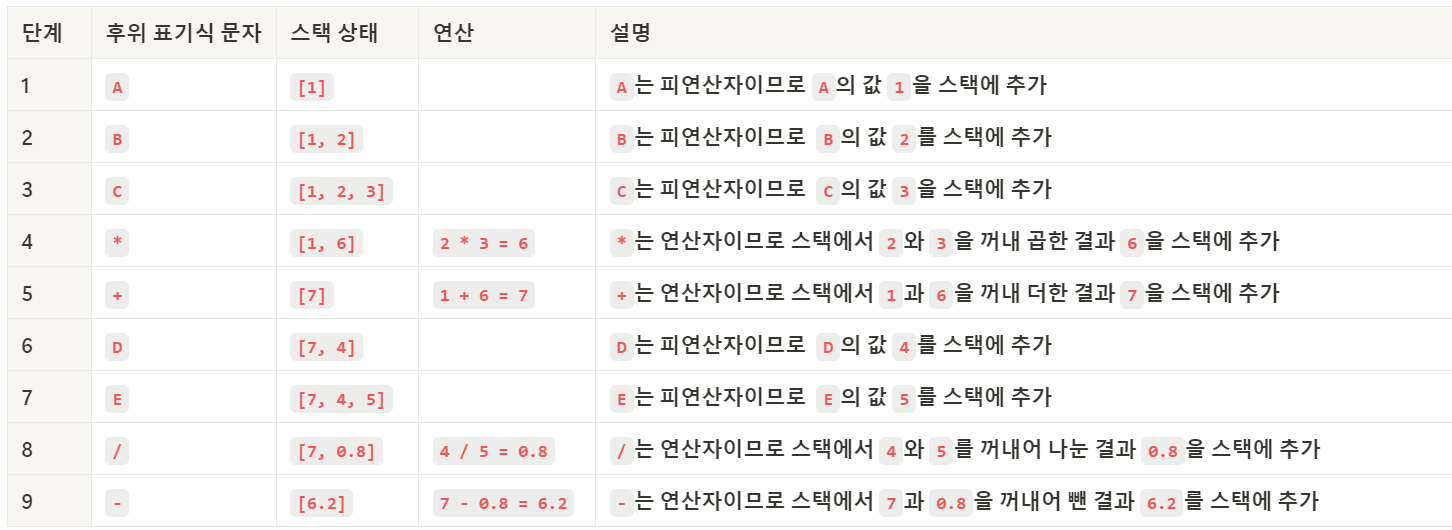
👩💻 나의 답안
import sys
input = sys.stdin.readline
n = int(input())
expression = input().strip()
values = [int(input().strip()) for _ in range(n)]
operand_values = {chr(65 + i): values[i] for i in range(n)}
stack = []
for char in expression:
if char.isalpha():
stack.append(operand_values[char])
else:
b = stack.pop()
a = stack.pop()
if char == "+":
stack.append(a + b)
elif char == "-":
stack.append(a - b)
elif char == "*":
stack.append(a * b)
elif char == "/":
stack.append(a / b)
result = stack.pop()
print(f"{result:.2f}")
✨ 새로 알게 된 점
1. 후위 표기식의 개념과 특징
후위 표기식은 연산자가 피연산자 뒤에 오는 방식으로, 예를 들어 A+B는 후위 표기식으로 AB+와 같이 표현됩니다.
후위 표기식의 가장 큰 장점은 연산 순서를 괄호 없이도 명확히 결정할 수 있다는 것인데 연산자와 피연산자의 순서만으로 계산 순서가 자연스럽게 정해지기 때문에 복잡한 수식도 중간 과정 없이 한 번에 계산이 가능합니다.
특히, 스택을 활용하면 후위 표기식을 더욱 쉽게 계산할 수 있습니다. 후위 표기식을 왼쪽에서 오른쪽으로 읽어가며 피연산자는 스택에 쌓고 연산자를 만나면 스택에서 값을 꺼내어 연산하는 방식이 매우 직관적이고 효과적이라는 점을 알게 되었습니다. 스택의 후입선출(LIFO) 구조가 후위 표기식의 계산 순서와 자연스럽게 맞아떨어져 연산 과정을 단순화하면서도 효율적으로 만들어줍니다.
728x90
'코딩테스트 대비' 카테고리의 다른 글
| [파이썬(Python)] 백준 10808번 알파벳 개수 (0) | 2024.11.15 |
|---|---|
| [파이썬(Python)] 백준 1918번 후위 표기식 (0) | 2024.11.14 |
| [파이썬(Python)] 백준 17299번 오등큰수 (0) | 2024.11.08 |
| [파이썬(Python)] 백준 17298번 오큰수 (0) | 2024.11.08 |
| [파이썬(Python)] 백준 10799번 쇠막대기 (0) | 2024.11.07 |